| zur Ergänzung von Teil II | Englisch | Kontakt |
Hier werden einige nützliche Hinweise zum Verständnis des Teils I gegeben.
| Inhalt |
1. Das Universum als expandierende Materiekugel
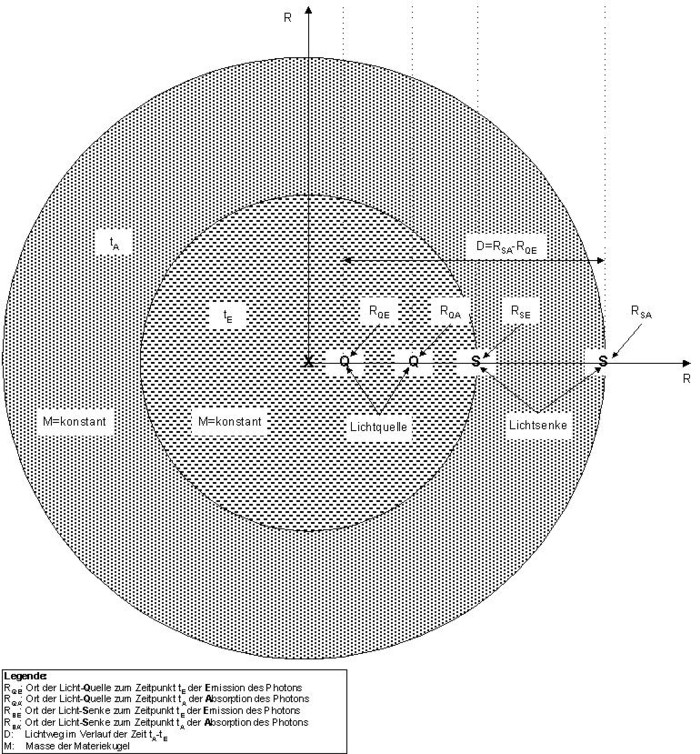
Für das bessere Verständnis der Ableitung der Hubble-Relation ist gewiß die folgende Abb. 1 nützlich:

|
Die Abbildung zeigt zweidimensionale Projektionen des sich ausdehnenden Universums zu zwei unterschiedlichen Zeitpunkten. Der innere Kreis entspricht der Ausdehnung R = RSE des Universums zum Zeitpunkt tE der Emission der Photonen einer beliebigen beobachteten Galaxie. Der größere Kreis zeigt die Ausdehnung R = RSA des Universums zum Zeitpunkt tA ( = heute) der Absorption dieser Photonen. Zu beachten ist, daß sich die Gesamtmasse MU des beobachtbaren Teils vom Universum wegen der Verwendung des Massenerhaltungssatzes bei der Lösung der Friedmnn-Gleichung immer vollständig innerhalb der jeweiligen Kugel mit dem Radius R = RSE bzw. R = RSA befindet und dort gleichmäßig verteilt ist.
Wenn die Friedmann-Gleichung, die die Entwicklung des Radius R der Materiekugel beschreibt, auf kosmologische Probleme tatsächlich anwendbar sein soll, muß sich der Beobachter auf der zugehörigen Kugeloberfläche befinden. Die beobachtbaren extragalaktischen Objekte sind dann an beliebigen Orten innerhalb der Massenkugel lokalisiert (durch RQE bzw. RQA ausgedrückt). Hierdurch ist sichergestellt, daß alle in die Modellvorstellung eingehenden Größen (Masse MU, Radius R und scheinbare Entfernung D) physikalisch sinnvoll miteinander verbunden sind. Auch sei vermerkt, daß die Photonen nur hierdurch den maximalen Lichtweg D = Dmax = DA = RSA (für diesen Fall gilt gerade RQE = 0) erreichen können. - In den Modellvorstellungen der Literatur wird der Beobachter irgendwo innerhalb der Materiekugel plaziert, und jede beobachtbare Galaxie bekommt über rQ = 0 (entspricht RQE = SE rQ = 0) stets gerade den Koordinatenursprung zugewiesen. Beides ist ganz offensichtlich falsch, da hierbei der Einfluß der Gesamtmasse nicht richtig berücksichtigt wird. Die Friedmann-Gleichung beschreibt auf Grund der Verschmelzung mit dem Massenerhaltungssatz die Entwicklung des Radius R der gesamten Materiekugel und nicht den in der Literatur benutzten Ort eines Beobachters irgendwo innerhalb dieser Kugel, der jeweils als Radius einer kleineren Kugel interpretiert werden kann, die dann nicht die Gesamtmasse enthält (jede beobachtete Galaxie befindet sich ja hier im Koordinatenursprung der gerade betrachteten Kugel).
Der von den beobachteten Photonen zurückgelegte Weg, der als scheinbarer Abstand allein für die Abschwächung der Helligkeit verantwortlich ist, ergibt sich gerade aus der Differenz D = RSA - RQE (man beachte hierbei, daß R = RSA = DA der heutige Kugelradius ist, aber RQE der Ort der emittierenden Galaxie irgendwo innerhalb der Massenkugel zum Zeitpunkt tE!). Das Licht benötigt für diesen Weg eine bestimmte Zeit. Während dieser Zeit wächst der Radius R der Massenkugel gemäß der Friedmann-Gleichung. Durch diese Expansion, die zeitlich parallel zur Photonenwanderung abläuft, wird die im Teil I der Aufsatzreihe behandelte Rotverschiebung erzeugt.
2. Zum "Verständnisproblem"
Um das nach der Gleichung (I, 22) erwähnte "Verständnisproblem" etwas näher zu erläutern, werden hierzu noch einige Hinweise gegeben.
2.1 Zum Massenerhaltungssatz
Für die allgemeinste Beschreibung der Masse M einer kugelförmigen Materieverteilung gilt das folgende Integral:
| (1) | 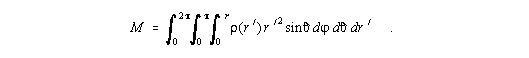
|
| (2) | 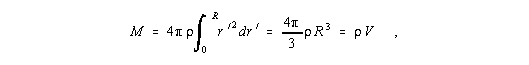
|
Genaugenommen wird die Expansion des Universums erst durch die Verwendung des Massenerhaltungssatzes bei der Lösung der Friedmann-Gleichung in die Theorie eingeführt! Mit anderen Worten: Wer eine Expansion sät, braucht sich nicht zu wundern, wenn er sie dann auch erntet.
2.2 Zum Kugelmodell des Universums
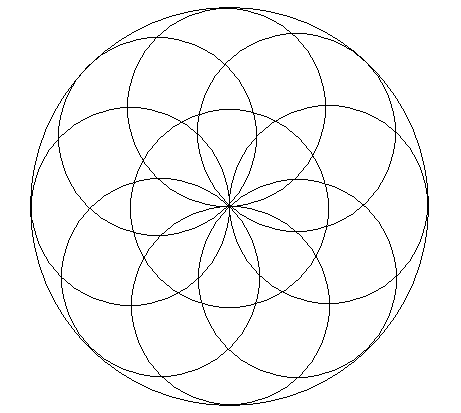
Das dem Beobachter meßtechnisch zugängige Universum können wir uns etwa gemäß der folgenden einfachen Abb. 2 vorstellen:
|
Obwohl der Beobachter nur einen Bereich überschauen kann, der der inneren kleinen Kugel entspricht (die auch die Masse M besitzt), hat das Universum mindestens die Größe der äußeren großen Kugel, da auf der vom Beobachter abgewandten Seite der Kugelmittelpunkte der kleinen Kugeln ebenfalls Materie sein muß, die ihm allerdings verborgen bleibt. Wird nun die Gültigkeit des Kosmologischen Prinzips hinzugenommen, folgt unmittelbar, daß das Universum als Ganzes unendlich groß ist. Um das einzusehen, denke man sich einen Beobachter, der sich z.B. einen Kugelradius entfernt von der Mitte der Abb. 2 aufhält: Er wird sich eine ähnliche Zeichnung vom Universum anfertigen, wie der erste Beobachter. Hierdurch "verschiebt" sich aber der Rand der großen Kugel ebenfalls um einen Kugelradius, d.h. für einen äußeren Beobachter erscheint das Universum entsprechend größer. Akzeptieren wir diese Aussage nicht, müssen wir annehmen, daß wir uns als Beobachter auf der Erde (innerhalb unserer Galaxis) gerade im Mittelpunkt der Welt befinden, was in uns mittelalterliche Gedanken erzeugt. Eine andere Möglichkeit ist natürlich, die Friedmann-Gleichung zu verwerfen. Dann müßten wir uns aber ein völlig neues und vielleicht auch besseres kosmologisches Modell ausdenken.
Eigentlich beschreibt die Friedmann-Gleichung die zeitliche Entwicklung des Radius von nur einer einzigen Materiekugel, die eine eindeutige Oberfläche besitzt. Außerhalb dieser Oberfläche befindet sich nach dieser Gleichung keine Materie, da die gesamte Masse M gemäß Gleichung (I, 5) innerhalb der Kugel lokalisiert sein muß. Der einzige Ausweg (den ich erkennen kann), die Friedmann-Gleichung für kosmologische Zwecke verwenden zu können, ist deshalb die hier erläuterte Modellvorstellung vom Universum.
3. Die scheinbare Grenzhelligkeit für verschiedene mittlere absolute Helligkeiten
Da im ersten Aufsatz der heutige Grenzabstand zu DA = 3206 Mpc bestimmt werden konnte, kann über die Gleichung
| (I,22) | 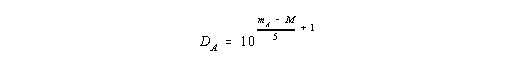
|
zu jeder durchschnittlichen absoluten Helligkeit <M> von extragalaktischen Objektgruppen (= Gruppen von Objekten mit ähnlichen physikalischen Eigenschaften, wie z.B. Quasare, Radio-Galaxien, gewöhnliche Galaxien, Supernovae Ia, ...) die zugehörige scheinbare Grenzhelligkeit mA berechnet werden. So ergibt sich für ausgewählte Werte der mittleren absoluten Helligkeit z.B.:
| mittlere absolute Helligkeit <M> | scheinbare Grenzhelligkeit mA |
| <M> = -19,00 | mA = 23,53 |
| <MG> = -19,91 | mAG = 22,62 |
| <M> = -20,00 | mA = 22,53 |
| <M> = -21,00 | mA = 21,53 |
| <M> = -22,00 | mA = 20,53 |
| <MQ> = -23,07 | mAQ = 19,46 |
Hier wurde für die mittlere absolute Helligkeit der Quasare die Bezeichnung <MQ> und für die gewöhnlichen Galaxien <MG> eingeführt. Entsprechend wurden mAQ bzw. mAG für die Bezeichnungen der zugehörigen scheinbaren Grenzhelligkeiten gewählt. Es ist zu erkennen, daß die scheinbare Grenzhelligkeit, bei der die Rotverschiebung unendlich wird, für die einzelnen Gruppen kosmischer Objekte unterschiedlich ausfällt.
Für eine im Schnitt besonders lichtschwache extragalaktische Objektgruppe kann demnach die scheinbare Grenzhelligkeit im Hubble-Diagramm durchaus sehr weit rechts liegen. Das schließt aber nicht aus, daß sich einzelne Gruppenmitglieder im Hubble-Diagramm rechts von mA aufhalten können, ohne unendlich rotverschoben zu sein. So werden z.B. jenseits von mAQ = 19,46 die weniger leuchtkräftigen Quasare beobachtet [vgl. hierzu die Abb. I,3], deren Anzahl beträchtlich ist.
Die Abb. 3 zeigt die zu den Werten der obigen Tabelle gehörenden theoretischen Kurven in einem einzigen Hubble-Diagramm vereint.
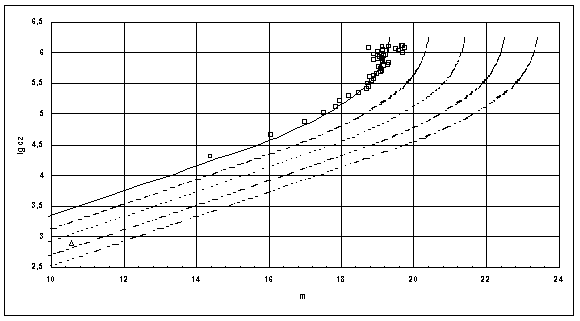
|
| Abb. 3: Hubble-Diagramm für teilweise fiktive Gruppen extragalaktischer Objekte, die sich durch
verschiedene mittlere absolute Helligkeiten <M> unterscheiden:
Von links nach rechts:
Bezeichnungen: |
| zur Ergänzung von Teil II | zurück zum Inhalt | Englisch | Kontakt |
Copyright by Steffen Haase, Greifswald (1998) and Leipzig (1999)
letzte inhaltliche Änderung: 31.12.2000
letzte Schreibfehlerkorrektur: 24.12.2006