| Englisch | Kontakt |
Zur Ableitung des Rotverschiebungsabstandes (Hubble-Gesetz):
Da ich den Eindruck habe, daß meine Ableitung des Hubble-Gesetzes nicht verstanden wurde
bzw. wird (siehe hierzu auch das Ablehnungsschreiben von "New Astronomy"), wird es an
dieser Stelle noch einmal abgeleitet, wobei einige zusätzliche Hinweise gegeben werden.
Die Ableitung des Hubble-Gesetzes im 1. Aufsatz ist natürlich richtig, sie ist aber vielleicht
nicht ausreichend verständlich dargestellt.
Hier können Sie das zugehörige Bild als ZIP-Datei (WinWord-Dokument) herunterladen.
Synonyme:
- Lichtquelle: ist irgendeine der beobachtbaren Galaxien; beobachtete Galaxie
- Lichtsenke: ist ein Meßinstrument, daß z.B. einem Beobachter auf der Erde (d.h. innerhalb
unserer Galaxis) gehört, in dem das beobachtete Photon absorbiert wird; Beobachtergalaxie
Verwendete Abkürzungen:
- ART: Allgemeine Relativitätstheorie
- SRT: Spezielle Relativitätstheorie
- RWM: Robertson-Walker-Metrik der ART
- Mpc: Megaparsec (in der Astronomie und Kosmologie übliche Dimension einer Länge)
Verwendete physikalische Größen und Variablen:
- t ist die Zeit
- r ist die zeitlich konstante Radialkoordinate der RWM; sie ist dimensionslos und hat keine
unmittelbare physikalische Bedeutung
- S(t) ist der zeitlich variable Skalenfaktor, der für die Expansion aller Maßstäbe verantwortlich
ist
- R(t) ist das zeitabhängige Produkt aus Skalenfaktor und RWM-Radialkoordinate, d.h. es gilt
R(t) = S(t) r. R(t) beschreibt einen zeitabhängigen radialen physikalischen Ort. Wenn wir dieser
radialen Ortskoordinate die Maßeinheit cm (oder, was den Kosmologen lieber ist: Mpc)
zuordnen, bedeutet dies, daß S(t) dieselbe Dimension trägt.
Verwendete Indizes:
- E steht für Emission (des später beobachteten Photons)
- A steht für Absorption (des beobachteten Photons)
- Q steht für Licht-Quelle (beobachtete Galaxie)
- S steht für Licht-Senke (die Photonen absorbierendes Meßgerät eines Beobachters, der sich
auch innerhalb einer Galaxie befindet; Ort der Beobachtergalaxie)
Verwendete einfache Zuordnungen und Zusammenhänge:
- tA ist der Zeitpunkt der Absorption des beobachteten Photons
- tE ist der Zeitpunkt der Emission des später beobachteten Photons
- rQ ist die zeitlich konstante radiale RWM-Koordinate der Lichtquelle (zeitlich konstant
bedeutet, daß rQ zum Zeitpunkt der Lichtemission dieselbe Größe hat, wie zum Zeitpunkt der
Lichtabsorption im Meßgerät)
- rS ist die zeitlich konstante radiale RWM-Koordinate der Lichtsenke (zeitlich konstant: siehe
rQ)
- SA = S(tA) ist der Skalenfaktor zum Zeitpunkt der Absorption des beobachteten Photons
- SE = S(tE) ist der Skalenfaktor zum Zeitpunkt der Emission des beobachteten Photons
- RSE = SE rS = S(tE) rS ist der physikalische Ort des Lichtsenke zum Zeitpunkt tE
- RSA = SA rS = S(tA) rS ist der physikalische Ort des Lichtsenke zum Zeitpunkt tA
- RQE = SE rQ = S(tE) rQ ist der physikalische Ort des Lichtquelle zum Zeitpunkt tE
- RQA = SA rQ = S(tA) rQ ist der physikalische Ort des Lichtquelle zum Zeitpunkt tA
- RSA - RSE ist der Weg, den die Beobachtergalaxie im Zeitintervall t = tA - tE zurücklegt
- RQA - RQE ist der Weg, den die beobachtete Galaxie im Zeitintervall t = tA - tE zurücklegt
- RSA - RQE ist der scheinbare Abstand zwischen dem Ort der Lichtquelle zum Zeitpunkt tE und
der Lichtsenke zum Zeitpunkt tA; genau diesen Weg legt das sich mit konstanter
Lichtgeschwindigkeit c bewegende Photon im Zeitintervall t = tA - tE zurück, ehe es im
Meßgerät des Beobachters verschwindet (wir haben hier stillschweigend angenommen, daß für
die Lichtsenke rS > rQ gilt)
Eine etwas ausführlicher kommentierte Ableitung des Rotverschiebungsabstandes (Hubble-Gesetz):
Wir wollen nun schauen, wie mit Hilfe der soeben eingeführten physikalischen Größen das
Hubble-Gesetz abgeleitet werden kann.
Die Gleichung (I,1) zeigt die RWM in ihrer allgemeinsten Ausprägung, d.h. in dieser Form ist
sie für die nicht-euklidische Geometrie gültig:
| (I,1) | 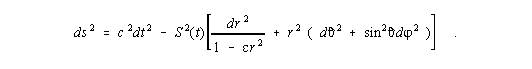
|
Die Krümmungskonstante kann die Werte ±1 bzw. 0 annehmen, wobei die Null für den euklidischen Raum gilt, auf den wir uns sogleich beschränken werden, da die Messungen der Astrophysiker auf ein flaches Universum hinweisen [und zugleich die Ableitung des Hubble-Gesetzes etwas einfacher wird :-)]. Vielleicht hilft es dem Leser, wenn er sich die Radialkoordinate der RWM als eine radiale Abstandskoordinate innerhalb einer Einheitskugel vorstellt, die, wie es der Name schon sagt, einen Radius mit dem Wert 1 hat (diese Annahme ist besonders einsichtig, wenn wir e = 1 setzen). Hierdurch gilt ein physikalisch sinnvoller Bereich von 0 £ r < 1. Die Galaxien vom Universum können wir uns dann in allen radialen Richtungen bei den unterschiedlichsten Werten von r angeheftet vorstellen (sie ruhen im Koordinatensystem der RWM!), wobei die eigentliche Größe des Universums (und hierdurch auch die Abstände zwischen den Galaxien) durch den aktuellen Wert des Skalenfaktors festgelegt wird. Dies veranschaulicht auch die Gleichung
| (I,2) | 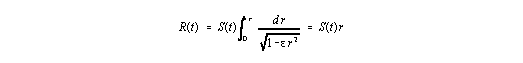
|
für e = 0.
Mit Hilfe der RWM folgt aus den Einsteinschen Gleichungen die Friedmann-Gleichung, die wir weiter unten benutzen werden.
Für ein sich mit konstanter Lichtgeschwindigkeit kräftefrei durch den euklidischen Raum bewegendes Photon gilt
| (I,10) | 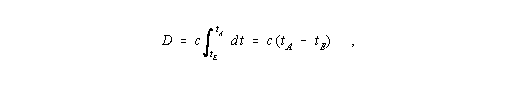
|
| (I,7) | 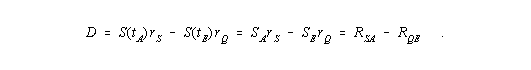
|
| (I,20) | 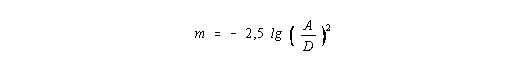
|
Die kosmologische Rotverschiebung wird durch
| (I,9) | 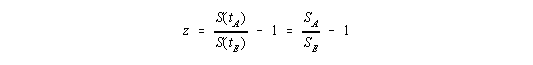
|
Nun wenden wir uns der Friedmann-Gleichung
| (I,11) | 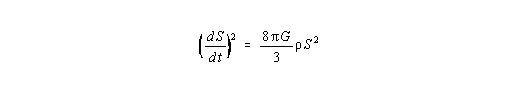
|
| (I,5) | 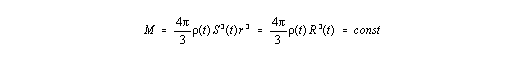
|
| (I,13) | 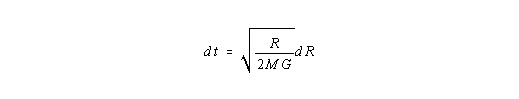
|
| (I,14) | 
|
| (I,15) | 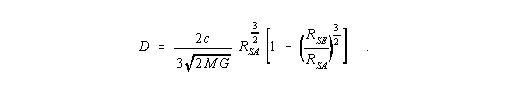
|
| (I,16) | 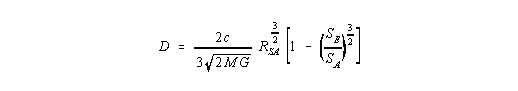
|
| (I,17) | 
|
| (I,18) | 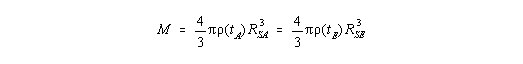
|
| (I,19) | 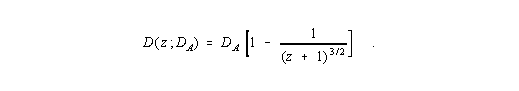
|
| (I,19a) | 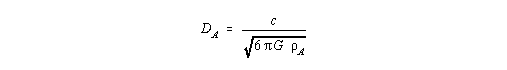
|
Die Friedmann-Gleichung hat in der Newtonschen Physik eine einfache physikalisch
anschauliche Bedeutung: Sie beschreibt die zeitliche Entwicklung des Radius R einer
Materiekugel. Genau dieselbe Bedeutung hat sie natürlich auch in der relativistischen
Kosmologie, die ja die Newtonsche Kosmologie als Näherung enthält. Die Friedmann-Gleichung beschreibt auf keinen Fall irgendwelche Abstände zwischen den Bestandteilen
dieser Massenkugel. Dies sollten wir uns stets vor Augen halten (der Leser vergleiche hier mit
dem ersten Abschnitt vom vierten Aufsatz).
Mit dem Erhalt der Gleichung (I,19) ist das wesentliche Ziel des ersten Aufsatzes erreicht. Der theoretische Rest des Aufsatzes beschäftigt sich nur mit der Umformung der Gleichung (I,19), um die den Astrophysikern zugängigen optischen Meßgrößen zu berücksichtigen. Hier setzt ein Kritikpunkt aus dem Ablehnungsschreiben von "New Astronomie" an: Es wird bezweifelt, daß D wirklich mit dem in den optischen Gleichungen benötigten Abstand übereinstimmt. Im Prinzip wurde auf dieses Problem weiter oben schon eingegangen: Der Abstand ist hier ein scheinbarer, der durch den vom Photon zurückgelegten Weg vermittelt wird. Da wir hier keinerlei Raumkrümmung berücksichtigt haben, gilt für den Lichtweg die einfache Formel D = ct und auch das einfache Intensitätsgesetz der klassischen Elektrodynamik. Deshalb ist alles in bester Ordnung, und bezüglich der Photonen ist genügend Relativität (so ein weiterer Kritikpunkt des schon genannten Ablehnungsschreibens) berücksichtigt worden. Man könnte meinen, daß die hier verwendete Friedmann-Gleichung nicht ausreichend Relativität enthält. Dies ist aber auch nicht der Fall, da diese Gleichung in der allgemein-relativistischen Kosmologie genauso aussieht, wie in der klassischen Kosmologie nach Newton. Im Übrigen sollten wir uns gerade darüber stark wundern, weil die begrenzte Lichtgeschwindigkeit in der ART und der zugehörigen Kosmologie keine direkte Wirkung zeigt! Genau dieser Umstand verleitet die heutigen Standard-Kosmologen dazu, sich mit einem äußerst spekulativen Urknall zu beschäftigen, der in kosmologischer Frühzeit ein Universum mit unendlicher Dichte und Temperatur zuläßt bzw. verlangt, und das auch noch in einem unendlich kleinen Volumen. Ich glaube, hierüber sollte jeder ernsthaft auf diesem Gebiet arbeitende Wissenschaftler einmal ganz scharf nachdenken. Ein sehr ähnlich gelagertes Problem hat übrigens die "Physik" der sogenannten Schwarzen Löcher. .....
| Englisch | Kontakt |
Copyright by Steffen Haase, Leipzig (2001)
letzte inhaltliche Änderung: 02.03.2005
letzte Schreibfehlerkorrektur: 13.05.2005