An dieser Stelle gehen wir etwas näher auf die Hintergründe des in dieser Aufsatzreihe vorgestellten kosmologischen Modells ein.

 

In der ursprünglichen Ausprägung (I,12)

 

 

beschreibt die Friedmann-Gleichung eine sich mit der Zeit verändernde gleichmäßig und kugelförmig verteilte Massendichte r(t), wobei sich diese Dichte entsprechend des sich zeitlich entwickelnden Radius R(t) der Massenverteilung verändert. Da außerdem der Massenerhaltungssatz (I,5)

 

 

gilt, beschreibt die Friedmann-Gleichung in der Form (I,13)

 

 

eine Materiekugel (Friedmann-Kugel), deren Radius R(t) sich mit der Zeit ändert.

Je nach ausgewählter Masse (Radius zu einer bestimmten, aber beliebig ausgewählten Zeit bei überall gleicher Materiedichte) werden sich die Radien der Kugeln unterschiedlich schnell vergrößern. Die Abbildung 1 zeigt beispielhaft die zeitliche Entwicklung von drei Kugeln mit verschiedenen Massen.

 

 

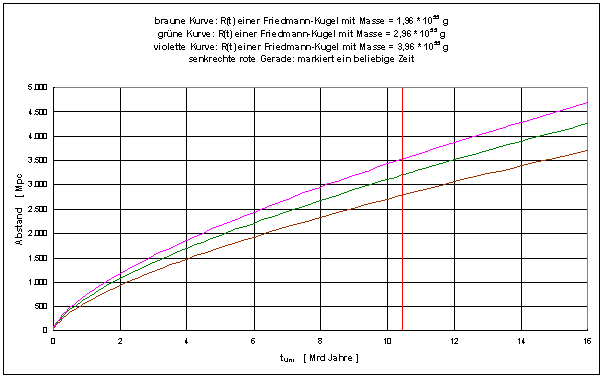
Abbildung 1

 

Die braune Kurve repräsentiert die kleinste und deshalb leichteste der hier gewählten Kugeln mit der Masse M = 1,96 * 1055 g. Sie dehnt sich nicht so schnell aus, wie die schwerste für diese Abbildung ausgewählte Kugel mit M = 3,96 * 1055 g (violette Kurve). Die grüne Kurve beschreibt eine Friedmann-Kugel mit der Masse M = 2,96 * 1055 g.

Wie groß diese Friedmann-Kugel (der jedem beliebigen Beobachter sichtbare Teil vom Universum) heute tatsächlich ist, zeigt der Vergleich der Theorie mit den astrophysikalischen Messwerten.

 

Wir wollen nun untersuchen, was genau hinter der hier gegebenen Ableitung des Hubble-Gesetzes steckt. Diesem Zweck dienen die folgenden zwei Abbildungen.

 

 

Abbildung 2

 

Die Abbildung 2 veranschaulicht das in die Ebene projizierte Universum von eigentlich unendlicher Größe, wobei die graue Hinterlegung die räumlich konstante Materiedichte r(t), die das Universum zu einem beliebig herausgegriffenen Expansionszeitpunkt t besitzt, darstellt.

Die abgebildeten Kreise entsprechen Projektionen von 4 beliebig ausgewählten Friedmann-Kugeln mit entsprechendem Materieinhalt (Massen Mi) zu diesem Zeitpunkt t.

Die blauen Pfeile, die jeweils vom Zentrum R = 0 der Kugeln in Richtung der Peripherie einer jeden gezeichneten Kugel zeigen, entsprechen dem Weg, der von Photonen während der bisher vergangenen Expansionszeit t des Universums zurückgelegt werden konnte, wenn sich diese immer mit der Lichtgeschwindigkeit c durch das Universum bewegt haben.

Wenn wir annehmen, dass sich auch die gravitative Wechselwirkung nur mit der Lichtgeschwindigkeit c ausbreiten kann, ist zu erkennen, dass die Kugeln I, II und III zum Zeitpunkt t gravitativ gebunden sind. Dies meint, dass im Verlauf der Expansion alle Bestandteile der Kugeln von den sich mit Lichtgeschwindigkeit ausbreitenden Gravitonen (den Bosonen der Gravitation) vom Zentrum der Kugel aus erreicht werden konnten. Für die Kugel IV trifft diese gravitative Gebundenheit nicht zu, weil sie einfach zu groß gewählt worden ist.

Eine Kosmologie, die den Anspruch erhebt, das Universum (bzw. den sichtbaren Teil davon) einigermaßen richtig zu beschreiben, darf Friedmann-Kugeln, die größer als die hier abgebildete Kugel III sind, nicht zulassen. Hierdurch fällt eine große Anzahl möglicher Kugeln aus der Betrachtung heraus.

 

Wichtig ist nun, dass bei der hier dargestellten theoretischen Ableitung des Rotverschiebungsabstandes (Hubble-Gesetz) genau die Kugel III herausgefiltert wird. Erreicht wird dieses Ziel durch das Gleichsetzen der beiden Zeitintervalle der Gleichungen (I,10) und (I,14). Außerdem bedeutet diese Gleichsetzung, dass es zu jedem Expansionszeitraum auch einen passenden Lichtweg gibt, der vom Beobachter zeitlich zurückblickend wahrgenommen werden kann.

Die tatsächliche Größe (Radius) dieser speziellen Kugel ergibt sich aus dem Vergleich des theoretisch abgeleiteten Hubble-Gesetzes mit einem durch Messungen gewonnenen Hubble-Diagramm.

 

Kommen wir nun zur nächsten Abbildung.

 

 

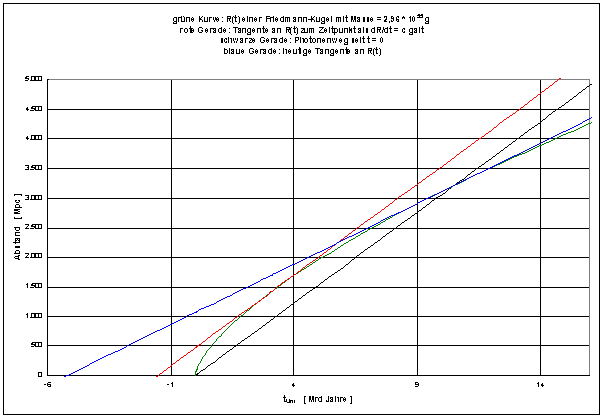
Abbildung 3:

 

In der Abbildung 3 beschreibt die grüne Kurve die Friedmann-Kugel, die sich beim Vergleich des hier abgeleiteten Hubble-Gesetzes mit einem Hubble-Diagramm ergibt (vgl. hierzu den ersten Aufsatz). Diese Kugel hat die Masse M = 2,96 * 1055 g.

Durch das Gleichsetzen der Zeitintervalle von Gleichung (I,10) und (I,14) in Gleichung (I,15) wird der rechte Schnittpunkt der Lichtweggleichung R = ct (schwarze Gerade) mit der Kurve R(t) der Friedmann-Kugel festgelegt. Hierdurch lässt sich die aktuelle Größe der Friedmann-Kugel bestimmen und auch der Zeitraum der bisherigen Expansion, das derzeitige Weltalter. Die auf diesem Weg gefundene Materiekugel ist heute gravitativ gebunden [1].

 

Die rote Gerade ist eine Parallele zur Lichtweggeraden. Ihr Schnittpunkt mit der grünen Kurve markiert den Schwarzschild-Zeitpunkt tS = 3,1 * 109 Jahre, zu dem die herausgefilterte Friedmann-Kugel gerade mit Lichtgeschwindigkeit c expandierte und ihr Radius dem Schwarzschild-Radius RS = 2MG/c2 = 1424 Mpc entsprach (vgl. mit dem vierten Aufsatz). Vor diesem Zeitpunkt war die Ausdehnungsgeschwindigkeit noch größer; sie war zur Zeit t = 0 sogar unendlich groß!

Es ergibt sich sofort die generelle Frage nach der gravitativen Gebundenheit der Masse innerhalb der Kugel vor diesem Schwarzschild-Zeitpunkt. Damit im Zusammenhang steht die wichtige Frage nach der tatsächlichen Ausbreitungsgeschwindigkeit der gravitativen Wechselwirkung. Wir könnten vermuten, dass sich die Gravitation instantan ausbreitet. Dies ist kein spezielles Problem des hier vorgestellten kosmologischen Modells, es betrifft jegliche Kosmologie, die auf der Verwendung der Robertson-Walker-Metrik fußt!

 

Die blaue Gerade ist die heutige Tangente an die grüne Kurve. Die Differenz zwischen dem Heute tA = 10,46 * 109 Jahre und dem Schnittpunkt dieser Geraden mit der Zeitachse markiert die Hubble-Zeit tH = 15,7 * 109 Jahre. Diese Zeit entspricht demnach nicht dem Alter vom Universum; sie besagt nur, dass das Universum die heutige Größe nach dieser Zeit erreicht hätte, wenn es sich immer mit der heutigen Expansionsgeschwindigkeit ausgedehnt hätte. Das Universum ist auf jeden Fall jünger, als es die Hubble-Zeit angibt.

 

Werden keine Überlichtgeschwindigkeiten in der Vergangenheit zugelassen (vgl. Teil IV der Aufsatzreihe), war das Universum nie kleiner als zum Schwarzschild-Zeitpunkt, für den die Expansionsgeschwindigkeit gerade der Lichtgeschwindigkeit entsprach (es galt immer R ³ RS). Hierdurch begann die Expansion nicht vor diesem Zeitpunkt tS und das Universum kann durchaus unendlich alt sein. Möglicherweise zog es sich vor diesem Zeitpunkt bis zur Größe R = RS zusammen, aber eben nicht weiter. Einen Urknall kann es dann nicht gegeben haben.

 

 

 

 

Copyright:
Dieser Text untersteht dem deutschen und internationalen Urheberrecht, d.h. die Veröffentlichung, Übersetzung, Übertragung auf andere Medien etc. - auch von Teilen - ist nur nach vorheriger Genehmigung des Autors gestattet. 

 

Copyright by Steffen Haase, Greifswald (1998) and Leipzig (1999)

 

 

Letzte inhaltliche Änderung:            15.10.2006
Letzte Schreibfehlerkorrektur:           15.10.2006

 


[1] Zugleich lässt die Abbildung erkennen, dass diese gravitative Gebundenheit nicht immer gegeben war, weil es einen Zeitraum gab, während dessen die Kugel schneller als mit Lichtgeschwindigkeit expandierte. Genau diese Möglichkeit der Friedmann-Gleichung betrachte ich als den wesentlichsten Fehler, der sich durch die Verwendung der Robertson-Walker-Metrik ergibt, die zur Friedmann-Gleichung führt, die wiederum die Ausbreitungsgeschwindigkeit der gravitativen Wechselwirkung nicht auf die Lichtgeschwindigkeit begrenzt, die die Lichtgeschwindigkeit eigentlich nicht enthält! - Da auch bei meiner Ableitung des Hubble-Gesetzes die Robertson-Walker-Metrik verwendet wird, muss auch ich zurzeit mit dieser nicht unerheblichen Merkwürdigkeit leben. .....